1.旅行终点站
题目
给你一份旅游线路图,该线路图中的旅行线路用数组 paths 表示,其中 paths[i] = [cityAi, cityBi] 表示该线路将会从 cityAi 直接前往 cityBi 。请你找出这次旅行的终点站,即没有任何可以通往其他城市的线路的城市。
题目数据保证线路图会形成一条不存在循环的线路,因此只会有一个旅行终点站。
示例 1:
输入:paths = [["London","New York"],["New York","Lima"],["Lima","Sao Paulo"]]
输出:"Sao Paulo"
解释:从 "London" 出发,最后抵达终点站 "Sao Paulo" 。本次旅行的路线是 "London" -> "New York" -> "Lima" -> "Sao Paulo" 。示例 2:
输入:paths = [["B","C"],["D","B"],["C","A"]]
输出:"A"
解释:所有可能的线路是:
"D" -> "B" -> "C" -> "A".
"B" -> "C" -> "A".
"C" -> "A".
"A".
显然,旅行终点站是 "A" 。示例 3:
输入:paths = [["A","Z"]]
输出:"Z"提示:
1 <= paths.length <= 100paths[i].length == 21 <= cityAi.length, cityBi.length <= 10cityAi != cityBi- 所有字符串均由大小写英文字母和空格字符组成。
思路
在所有的点寻找没有出度的点,用一个 set 保存所有路径的起点,那么不在 set 中的点即为所求。
class Solution {
public String destCity(List<List<String>> paths) {
Set<String> set = new HashSet<>();
for(List<String> list : paths) {
set.add(list.get(0));
}
for(List<String> list : paths) {
if(!set.contains(list.get(1))) {
return list.get(1);
}
}
return "";
}
}2.是否所有 1 都至少相隔 k 个元素
题目
给你一个由若干 0 和 1 组成的数组 nums 以及整数 k。如果所有 1 都至少相隔 k 个元素,则返回 True ;否则,返回 False 。
示例 1:
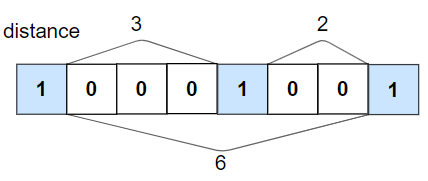
输入:nums = [1,0,0,0,1,0,0,1], k = 2
输出:true
解释:每个 1 都至少相隔 2 个元素。示例 2:
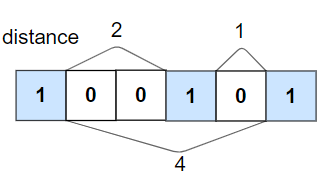
输入:nums = [1,0,0,1,0,1], k = 2
输出:false
解释:第二个 1 和第三个 1 之间只隔了 1 个元素。示例 3:
输入:nums = [1,1,1,1,1], k = 0
输出:true示例 4:
输入:nums = [0,1,0,1], k = 1
输出:true提示:
1 <= nums.length <= 10^50 <= k <= nums.lengthnums[i]的值为0或1
思路
使用 pre 保存前一个 1 的索引,每次遇见 1 则比较当前索引 i 和 pre 的差值是否大于 k 并更新 pre。
class Solution {
public boolean kLengthApart(int[] nums, int k) {
int pre = -1;
for(int i = 0; i < nums.length; i++) {
if(nums[i] == 1) {
if(pre == -1) {
pre = i;
} else if(i - pre <= k) {
return false;
} else {
pre = i;
}
}
}
return true;
}
}3.绝对差不超过限制的最长连续子数组
题目
给你一个整数数组 nums ,和一个表示限制的整数 limit,请你返回最长连续子数组的长度,该子数组中的任意两个元素之间的绝对差必须小于或者等于 limit 。
如果不存在满足条件的子数组,则返回 0 。
示例 1:
输入:nums = [8,2,4,7], limit = 4
输出:2
解释:所有子数组如下:
[8] 最大绝对差 |8-8| = 0 <= 4.
[8,2] 最大绝对差 |8-2| = 6 > 4.
[8,2,4] 最大绝对差 |8-2| = 6 > 4.
[8,2,4,7] 最大绝对差 |8-2| = 6 > 4.
[2] 最大绝对差 |2-2| = 0 <= 4.
[2,4] 最大绝对差 |2-4| = 2 <= 4.
[2,4,7] 最大绝对差 |2-7| = 5 > 4.
[4] 最大绝对差 |4-4| = 0 <= 4.
[4,7] 最大绝对差 |4-7| = 3 <= 4.
[7] 最大绝对差 |7-7| = 0 <= 4.
因此,满足题意的最长子数组的长度为 2 。示例 2:
输入:nums = [10,1,2,4,7,2], limit = 5
输出:4
解释:满足题意的最长子数组是 [2,4,7,2],其最大绝对差 |2-7| = 5 <= 5 。示例 3:
输入:nums = [4,2,2,2,4,4,2,2], limit = 0
输出:3提示:
1 <= nums.length <= 10^51 <= nums[i] <= 10^90 <= limit <= 10^9
思路
滑动窗口,使用单调队列维护当前窗口的最大值和最小值,保持最大值与最小值的差小于 limit 即可
class Solution {
public int longestSubarray(int[] nums, int limit) {
if(nums.length == 1) {
return 1;
}
int ans = 0;
int n = nums.length;
LinkedList<Integer> max = new LinkedList<>();
LinkedList<Integer> min = new LinkedList<>();
int left = 0;
int right = 1;
max.addLast(left);
min.addLast(left);
while(right < n) {
if(nums[max.getFirst()] - nums[min.getFirst()] <= limit) {
while(!max.isEmpty() && nums[max.getLast()] < nums[right]) {
max.removeLast();
}
max.addLast(right);
while(!min.isEmpty() && nums[min.getLast()] > nums[right]) {
min.removeLast();
}
min.addLast(right);
right++;
} else {
if(max.getFirst() == left) {
max.removeFirst();
}
if(min.getFirst() == left) {
min.removeFirst();
}
left++;
}
if(nums[max.getFirst()] - nums[min.getFirst()] <= limit) {
ans = Math.max(ans, right-left);
}
}
return ans;
}
}4.有序矩阵中的第 k 个最小数组和
题目
给你一个 m * n 的矩阵 mat,以及一个整数 k ,矩阵中的每一行都以非递减的顺序排列。
你可以从每一行中选出 1 个元素形成一个数组。返回所有可能数组中的第 k 个 最小 数组和。
示例 1:
输入:mat = [[1,3,11],[2,4,6]], k = 5
输出:7
解释:从每一行中选出一个元素,前 k 个和最小的数组分别是:
[1,2], [1,4], [3,2], [3,4], [1,6]。其中第 5 个的和是 7 。 示例 2:
输入:mat = [[1,3,11],[2,4,6]], k = 9
输出:17示例 3:
输入:mat = [[1,10,10],[1,4,5],[2,3,6]], k = 7
输出:9
解释:从每一行中选出一个元素,前 k 个和最小的数组分别是:
[1,1,2], [1,1,3], [1,4,2], [1,4,3], [1,1,6], [1,5,2], [1,5,3]。其中第 7 个的和是 9 。 示例 4:
输入:mat = [[1,1,10],[2,2,9]], k = 7
输出:12提示:
m == mat.lengthn == mat.length[i]1 <= m, n <= 401 <= k <= min(200, n ^ m)1 <= mat[i][j] <= 5000mat[i]是一个非递减数组

